Champ magnétique dans un solénoïde

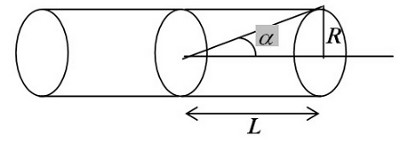
Solénoïde infini

Dans un solénoïde infini, le champ magnétique est uniforme et vaut partout dans le solénoïde : avec spires par unité de longueur

u.s.i.

I en Ampère

On obtient : pour I = 1 ampère

0 mT

Incertitude 2% ( mT)

Calcul théorique

½ Nb spires	½ Longueur (cm)	n = N/L		I = 1 A et en mT	I=1A et en mT
5	1,025	488	0,201	0,63	0,13
10	2,05	488	0379	0,63	0,24
20	4,15	482	0,639	0,63	0,40
30	6,225	482	0,78	0,63	0,49
50	10,375	482	0,901	0,63	0,568
70	14,55	481	0,946	0,63	0,596
100	20	500	0,97	0,63	0,61

Quelques précisions

Le champ dépend du nombre de spires n par unité de longueur (et non du nombre de spires N total sur une longueur L) qui est le même pour toutes les positions des fils (environs 500 spires par mètre : n = N/L)

Il y a 40 cm de bobine au maximun avec 200 spires soit 500 spires par unité de longueur. Pour les autres cas : n = 500 spires par unité de longueur

Pour une configuration donnée, le champ magnétique est proportionnel à l'intensité du courant (facile à vérifier normalement).

Au début du document, vous trouverez la valeur théorique du champ au milieu du solénoïde, avec la comparaison champ dans une bobine infiniment longue et une bobine finie : pour une bobine suffisamment longue, la correspondance est bonne.